IrregularPolygon

Background:

Polygons are closed two-dimensional shapes bounded by line segments. The segments meet in pairs at corners called vertices. A polygon is irregular if not all its sides are equal in length. The figure below shows examples of irregular polygons:

(Source: Intermath Dictionary, http://www.intermath-uga.gatech.edu/dictnary/descript.asp?termID=186)

Assignment:

1. Implement a class IrregularPolygon that contains an array list of Point2D.Double objects.

2. The Point2D.Double class defines a point specified in double precision representing a location in (x, y) coordinate space. For example, Point2D.Double(2.5, 3.1) constructs and initializes a point at coordinates (2.5, 3.1).

3. Use the following declarations as a starting point for your lab work.

   import java.awt.geom.*;     // for Point2D.Double
import java.util.ArrayList; // for ArrayList
import gpdraw.*;            // for DrawingTool

   public class IrregularPolygon{
   private ArrayList <Point2D.Double> myPolygon;

   // constructors
   public IrregularPolygon() { }

   // public methods
   public void add(Point2D.Double aPoint) { }

      public void draw() { }

      public double perimeter() { }

      public double area() { }
}

4. The program should use the Drawing Tool to draw the polygon by joining adjacent points with a line segment, and then closing it up by joining the end and start points.

5. Write methods that compute the perimeter and the area of a polygon. To compute the perimeter, compute the distance between adjacent points, and total up the distances. The area of a polygon with corners 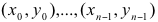is the absolute value of:

   

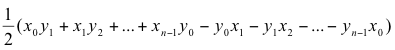
   Note: add n products, then subtract n products, then divide by 2. The result will be negative or positive depending on the order in which the products are taken, i.e., which products are subtracted and which are added.

6. As a test case, the parallelogram formed by the following coordinates has a perimeter of 174.1 units and an area of 1700 square units: (20, 10), (70, 20), (50, 50), (0, 40).