Polygons are two-dimensional shapes formed by line segments. The segments are edges that meet in pairs at corners called vertices. A polygon is regular if all its sides are equal and all its angles are equal.
For an n-sided regular polygon of side s, the angle at any vertex is q, and the radii of the inscribed and circumscribed circles are r and R respectively. A 5-sided regular polygon (pentagon) would be represented as follows:
-
Write two constructor methods. The default constructor creates a 3-sided polygon (triangle). The other constructor takes an integer value representing the number of sides and a double value representing the length of the sides and constructs the corresponding regular polygon.
- Write a method that calculates the vertex angle, q. This angle can be determined as follows:
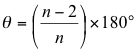
where n represents the number of sides.
- Write a method that calculates the perimeter. This value is determined simply as the number of sides, n, times the length of a side, s:
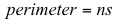
- Write a method that calculates the radius of the inscribed circle, r. The inscribed circle is the circle that can be drawn inside of the regular polygon such that it is tangent to every side of the polygon, for example, the smaller circle in the diagram above. It can be calculated as:
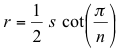
where n represents the number of sides, s represents the length of a side, and cot() is the trigonometric function, cotangent. We use the value π instead of 180 in the formula because the Java math functions assume that angles are given in radians instead of degrees. Note: the built-in Java method math.PI produces the value of π. An alternative is to replace π with 180 in all the formulas here and use following method from the Math Class to convert from degrees to radians:
Math.toRadians(double angdeg)
Write a method that calculates the radius of the circumscribed circle, R. The circumscribed circle is the circle that intersects each vertex of the polygon, for example the larger circle in the diagram above. R can be calculated as:
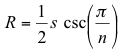
where n represents the number of sides, s represents the length of a side and csc() is the trigonometric function, cosecant. The cosecant function is not part of the Java Math Class, however, the cosecant of an angle can be calculated as the reciprocal of the sine as follows:
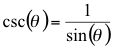
Write a method that calculates the area of the regular polygon. It can be calculated as:
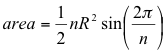
where n represents the number of sides and R represents the radius of the circumscribed circle.
-
All trigonometric function in the Java Math Class take radians as the parameter. To convert an angle measured in degrees to the equivalent angle measured in radians use the following method from the Math Class:
public static double toRadians(double angdeg)
Square: number of sides = 4, length of side = 10
Octagon: number of sides = 8, length of side = 5.75
Enneadecagon: number of sides = 19, length of side = 2
Enneacontakaihenagon: number of sides = 91, length of side = 0.5
Answers:



