-
The overall logic of mergeSort is to "divide and conquer." A list of random integers will be split into two or more equal-sized lists (each with the same number of elements, plus or minus one), with each partial list or “sublist” sorted independently of the other. The next step will be to merge the two sorted sublists back into one big sorted list.
-
Here is a non-recursive mergeSort method. We divide the list into two equal-sized parts and sort each with the selection sort, then merge the two using an algorithm to be discussed in part B.
/* List A is unsorted, with A.size() values in the ArrayList.
first is the index of the first value; last
is the index of the last value in the ArrayList;
first < last.
*/
void mergeSort (ArrayList <Integer> A, int first, int last){
int mid;
mid = (first + last) / 2;
selectionSort (A, first, mid);
selectionSort (A, mid+1, last);
merge (A, first, mid, last);
}
A modified selection sort will have to be written to sort a range of values in list A. Likewise, the merge method will have to be modified to internally merge two halves of the array into one ordered array.
The following example will illustrate the action of a non-recursive mergeSort on a section of a list containing 8 values:

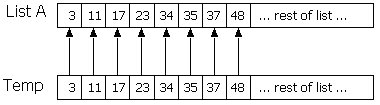
- Merging the two halves of the array in the modified merge method will require the use of a local temporary array. Because the two sublists are stored within one array, the easiest approach is to merge the two sublists into another array, then copy the temp array back to the original.

Then copy Temp back into List A:
- This version of
merge will need to be able to work with sections of ArrayList A. Here is a proposed parameter list for merge:
/* will merge the two sorted sublists within A into
one continuous sublist from A[first] .. A[last].
The left list ranges from A[first]..A[mid]. The
right list ranges from A[mid+1]..A[last].
*/
void merge (ArrayList <Integer> A, int first, int mid, int last)
The recursive version of mergeSort will require the above version of merge. However, to help you understand how to write a merge method, we next present a simpler merge algorithm.


