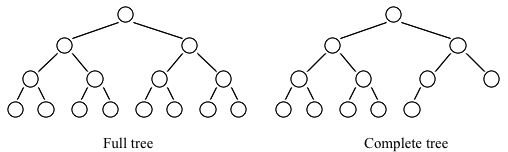
Heaps are based on the notion of a complete tree. A binary tree is called completely full if all its levels are filled with nodes. A binary tree is completely full if it is of height h, and has 2h-1 nodes. Each level contains twice as many nodes as the preceding level.
- A binary tree is termed complete if it has no gaps on any level. The last level may have some leaves missing on the right, as shown below:
A heap is a binary tree that satisfies two conditions:
- it is a complete tree
- the value in each node does not exceed any value in that node’s left and right subtrees
Heaps are allowed to have more than one data item with the same value, and values in the left subtree do not have to be ranked lower than values in the right subtree.
- A heap can be used as a priority queue: the highest priority item is at the root and is trivially found. But if the root is deleted, we are left with two sub-trees and we must efficiently re-create a single tree with the heap property. The value of the heap structure is that we can both extract the highest priority item and insert a new item in O(log n) time.


