- Removing an item from a priority queue is straightforward if the queue is represented by a binary heap. The next item to leave the queue will always be the item at the top (root) of the heap.
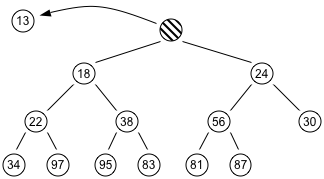
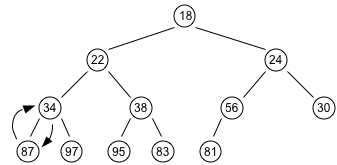
- The shape of the heap is restored by removing the last leaf and placing it into the root. For the heap shown below, the position that must become empty is the one occupied by the 87. This is placed in the vacant root position.
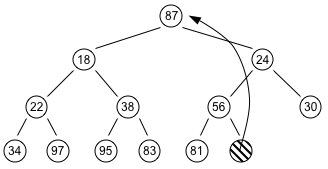
- This has violated the condition that the root must be greater than each of its children. To repair the order, we apply the “heapify” procedure in which the value from the root moves down the heap until it falls into place.
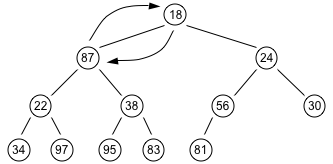
- At each step down the value 87 is swapped with its smaller child.
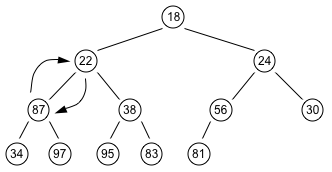
- The heap property still has not been restored in the left subtree. So again interchange the 87 with the smaller of its children.
-
We need to make at most h (recall that h is the height of the tree) interchanges of a root of a subtree with one of its children to fully restore the heap property. Thus deletion from a heap is O(log n).
- To add an item to a heap, we follow the reverse procedure. First we add the new node as the last leaf, and then apply a “reheap up” procedure to restore the ordering property of the heap. “Reheap up” moves the new node up the tree, swapping places with its parent until the order is restored. For example, adding the value 9 to the original heap would result in the following sequence of steps:
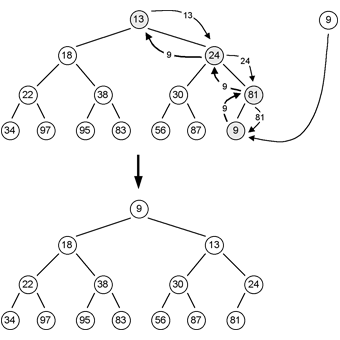
- Again, we require O(log n) exchanges.


